Merge sort
In computer science, merge sort (also commonly spelled mergesort) is an O(n log n) comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output.
Mergesort is a divide and conquer algorithm. Divide and conquer algorithms divide the original data into smaller sets of data to solve the problem.
During the Mergesort process the object in the collection are divided into two collections. To split a collection, Mergesort will take the middle of the collection and split the collection into its left and its right part. For more additional info Learn Java Online
The resulting collections are again recursively splitted via the Mergesort algorithm until they are broke to single element in each collection.
After splitting each collection, mergesort algorithm start combining all collections obtained via above procedure.
To combine both collections Mergesort start at each collection at the beginning. It pick the object which is smaller and inserts this object into the new collection.
For this collection it now selects the next elements and selects the smaller element from both collection by comparing one element from each collection at a time.
The Algorithm:
Merge sort is a “divide and conquer” algorithm wherein we first divide the problem into subproblems. When the solutions for the subproblems are ready, we combine them together to get the final solution to the problem. For more skills Java Online Classes
This is one of the algorithms which can be easily implemented using recursion as we deal with the subproblems rather than the main problem.
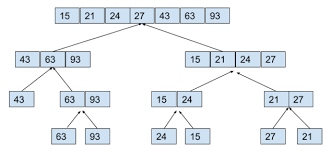
The algorithm can be described as the following 2 step process:
- Divide: In this step, we divide the input array into 2 halves, the pivot being the midpoint of the array. This step is carried out recursively for all the half arrays until there are no more half arrays to divide.
- Conquer: In this step, we sort and merge the divided arrays from bottom to top and get the sorted array.
When to use Merge Sort:
- Merge sort is used when the data structure doesn’t support random access, since it works with pure sequential access (forward iterators, rather than random access iterators). It’s also widely used for external sorting, where random access can be very, very expensive compared to sequential access.
For example, When sorting a file which doesn’t fit into memory, you might break it into chunks which fit into memory, sort these using independently, writing each out to a file, then merge sort the generated files. For Practical Programming core java online course
- Also, you can use merge sort when you need a stable sort. It’s very important feature of merge sort.
- Mergesort is quicker when dealing with linked lists. This is because pointers can easily be changed when merging lists. It only requires one pass (O(n)) through the list.
- If there is a lot of parallelization occurs then parallelizing Mergesort is simpler than other sort algorithms.
Sorting Array using Merge Sort Algorithm:
You have given an unordered list of integers (or any other objects e.g. String), You have to rearrange the integers or objects in their natural order.
Example:
import java.util.Arrays;
/*
* Java Program to sort an integer array using merge sort algorithm.
*/
public class Main {
public static void main(String[] args) {
System.out.println("mergesort");
int[] input = { 87, 57, 370, 110, 90, 610, 02, 710, 140, 203, 150 };
System.out.println("array before sorting");
System.out.println(Arrays.toString(input));
// sorting array using MergeSort algorithm
mergesort(input);
System.out.println("array after sorting using mergesort algorithm");
System.out.println(Arrays.toString(input));
}
/**
* Java function to sort given array using merge sort algorithm
*
* @param input
*/
public static void mergesort(int[] input) {
mergesort(input, 0, input.length - 1);
}
private static void mergesort(int[] input, int start, int end) {
// break problem into smaller structurally identical problems
int mid = (start + end) / 2;
if (start < end) {
mergesort(input, start, mid);
mergesort(input, mid + 1, end);
}
// merge solved pieces to get solution to original problem
int i = 0, first = start, last = mid + 1;
int[] tmp = new int[end - start + 1];
while (first <= mid && last <= end) {
tmp[i++] = input[first] < input[last] ? input[first++] : input[last++];
}
while (first <= mid) {
tmp[i++] = input[first++];
}
while (last <= end) {
tmp[i++] = input[last++];
}
i = 0;
while (start <= end) {
input[start++] = tmp[i++];
}
}
}
To get in-depth knowledge, enroll for a live free demo on Java Online Training